The cost function in machine learning calculates the variation between real and anticipated output, assessing model accuracy and ensuring evenness. It's crucial for real-world applications. It has different types and specific importance.
This blog describes the meaning, types, and importance of cost functions in machine learning. Let’s begin!
Cost Function in Machine Learning – Interpretation
The cost function in machine learning is defined as the function that calculates the deviation between real output and anticipated output. It is also called the loss function.
On a broad range, the cost function assesses the accuracy of the model to map the input and output data relationship. It is very important to understand evenness and unevenness in a model for a given data set.
These models work with real-world applications. Therefore, minor errors can affect the overall calculation of a project, and one may suffer losses.
For example,
If we consider someone who wants to start a cookie business and, before that, they want to prepare the perfect recipe for baking cookies, they try different amounts of butter and sugar. As a result, they get too sweet or too dry cookies.
The cost function in machine learning is like a taste test for each batch. Hence, the cost function measures how away each batch is from the perfect required taste.
Here, the aim is to reduce the "cost" by adjusting the ingredients unless and until you get the best possible cookies.
Types of Cost Functions in Machine Learning
1. Mean Squared Error (MSE)
It is largely used as a basic estimation method in machine learning. In this method, square error values are combined, and then the total is taken for calculation. It is also known as the statistical model.
In this method, squares are taken so it eliminates all negative values. Hence, the distance-based faultiness issue gets resolved.
Formulae: MSE = (1/n) * Σ (y_i - ŷ_i)²

Where:
n is the number of samples,
y_i is the actual value,
ŷ_i is the predicted value.
2. Distance-Based Error
A distance-based error is the fundamental cost function that connects the concept for many kinds of cost functions.
Formulae: Distance-Based Error = |y_true - y_pred|

Where:
y_true - Actual or ground truth value for a specific observation.
y_pred - Predicted value generated by the model for that observation.
3. Root Mean Squared Error
The residuals' dispersion (prediction errors) is measured by the Root Mean Square Error, or RMSE. Relative to the regression line, the distance between the data points is expressed in terms of residuals, and the RMSE measures the distribution of these residuals.
Formulae: RMSE = sqrt( (1/n) * Σ (y_true,i - y_pred,i)² )
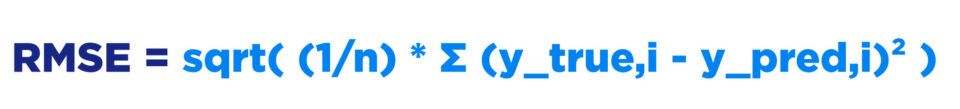
Where:
n - Total number of observations (data points) in the dataset.
y_true - Actual or ground truth value for a specific observation.
y_pred - Predicted value generated by the model for that observation.
4. Cross-Entropy Function
An information theory metric called cross-entropy expands on entropy by calculating the difference between various probability distributions.
Cross-entropy is a measure of the overall entropy between the populations as opposed to KL convergence, which calculates the comparative entropy between two probability density functions.
Formulae:
For binary classification:
Binary Cross-Entropy = -(1/n) * Σ (y_i * log(ŷ_i) + (1 - y_i) * log(1 - ŷ_i))
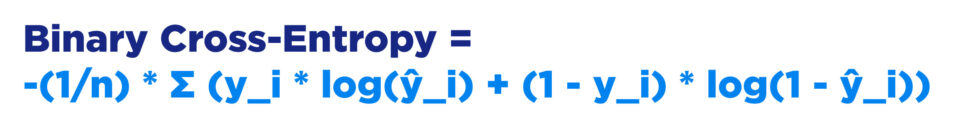
For multi-class classification:
Categorical Cross-Entropy = -Σ (y_i * log(ŷ_i))

Where:
C is the number of classes,
ŷ_i is the predicted probability of class i.
5. Mean Absolute Error
The mean deviation between the roughly computed values and real values is calculated using mean absolute error. As this method assesses the faultiness in field observations on the same scaling, it is also known as scale-dependent accuracy.
In regression analysis, the mean absolute error serves as the machine learning assessment indicator.
Formulae: MAE = (1/n) * Σ |y_i - ŷ_i|

Where:
n is the number of samples,
y_i is the actual value,
ŷ_i is the predicted value.
6. Kullback-Liebler (KL) Divergence
This function is very similar to cross entropy function. This method calculates the change among two probability density functions.
The procedure of calculating the KL divergence function includes two likelihood distributions.
Formulae: D_KL(P || Q) = Σ P(i) * log(P(i) / Q(i))

Where:
P is the true distribution and Q is the estimated distribution.
7. Hinge Loss
The hinge loss function is a common cost function utilized in Support Vector Machines (SVM) classification.
Formulae: Hinge Loss = (1/n) * Σ max(0, 1 - y_i * ŷ_i)

Where:
y_i is the true label (either -1 or 1).
Importance of cost function in machine learning
Cost function in machine learning
- Quantifies the error between anticipated and projected values to assess performance.
- Increases accuracy by directing the model to reduce mistakes and increase precision.
- Evaluates the link between input and output parameters to assess model performance.
- Comparing models or variants of the same model might be useful.
- Shows project achievement without requiring knowledge of the inner workings of the model.
Summing Up!
The cost function in machine learning is a function that calculates the variation between real and anticipated output. It assesses the accuracy of a model in mapping input and output data relationships. Cost functions include 7 different types, which we tried to explain.
We hope this blog content will clear your doubts regarding cost functions in machine learning. To get more knowledge-driven and tech-oriented content, keep visiting us at WisdomPlexus.
You may also like to Read:
Common Misconceptions About Machine Learning
The Important Unanswered Questions in Machine Learning (ML)




